予測や推計でモデルを使うときには、モデルが未知のデータに対して予測精度があるかを適切に検証しておくことが重要です。
今回の記事では、交通分野における従来のロジットモデルの検証方法を紹介するとともに、本来あるべきモデルの検証の考え方と方法を、「The overreliance on statistical goodness-of-fit and under-reliance on model validation in discrete choice models: A review of validation practices in the transportation academic literature」(以下、参考論文)を参考に紹介したいと思います。
なお、ロジットモデルの概要を知りたい方は、「都市交通とロジットモデル」の記事をご覧ください。
従来のモデルの検証方法
交通分野でのロジットモデルの検証は、統計的有意性、モデル全体の適合度、現況再現性の3つの視点で行われることが多いです。
統計的有意性
各説明変数が統計的に有意であるかどうかをt値やp値をもとに判断します。交通分野では慣習的に、有意水準5%以下であれば有意とすることが多く、t値の絶対値が1.96以上、p値が0.05以下が目安として、よく使われます。
また、統計的有意性とは直接関係ありませんが、各説明変数のパラメータの「符号条件」を確認することも、よく行われます。
例えば、交通手段の選択においては、所要時間のパラメータはマイナスである(所要時間が増えるほど、その交通手段は択ばれにくくなる)のが、仮説してあるため、この符号条件に合わないモデルは採用しないということを行います。
モデル全体の適合度
推定に使用した実績データに対するモデルの当てはまりの良さを示す指標として、尤度比、自由度調整済み尤度比、AIC、BIC、的中率等がよく用いられます。(各指標の詳細に関しては「検証の評価指標」の項目で記載)
現況再現性
推定に使用した実績データの選択確率とモデルから予測された選択確率を比較することで、現況再現性の確認を行います。
交通分野では、取得された実績データを全て使ってモデルを推定し、全てのデータに対して現況再現性を確認するということがよく行われてきましたが、この問題点に関しては、次で述べます。
従来の検証方法の問題点
交通分野では、取得された実績データを全て使ってモデルを推定し、全てのデータに対して現況再現性を確認するということがよく行われています。
これは、推定に用いたデータに対する当てはまりを見ているだけであり、未知のデータに対する検証を行っていないことになります。
また、全てのデータを使ってモデルを推定すると、そのデータに対して過剰にフィットしたモデルになってしまい、新しいデータに対しての予測精度が下がってしまう場合があります。
機械学習の分野では「過学習」と言われている現象であり、この過学習を避けるために、交差検証などの方法を用いることで、未知のデータに対する予測精度を検証しています。(過学習に関しては、例えばこちら等を参照ください)
参考論文によると、交通分野においては92%の論文で何らかの統計的な検証が行われてはいるが、機械学習の分野で行われているような交差検証等により未知のデータに対する予測精度の検証を行っているのは18.1%しかないと述べられています。
交通分野におけるモデルは、行動理解(どの説明変数が影響を与えるかの把握)に用いることもありますが、施策後や将来の変化を予測・理解するために用いられることも多く、特に実務においては予測結果が意思決定の判断材料として用いられています。
そのため、統計的有意性の確認や全データを対象にした再現性の検証だけではなく、未知のデータに対する予測精度を適切に評価しておくことが重要です。
以降では、検証の考え方と検証方法の概要について紹介をします。
検証の考え方と検証方法
検証の考え方
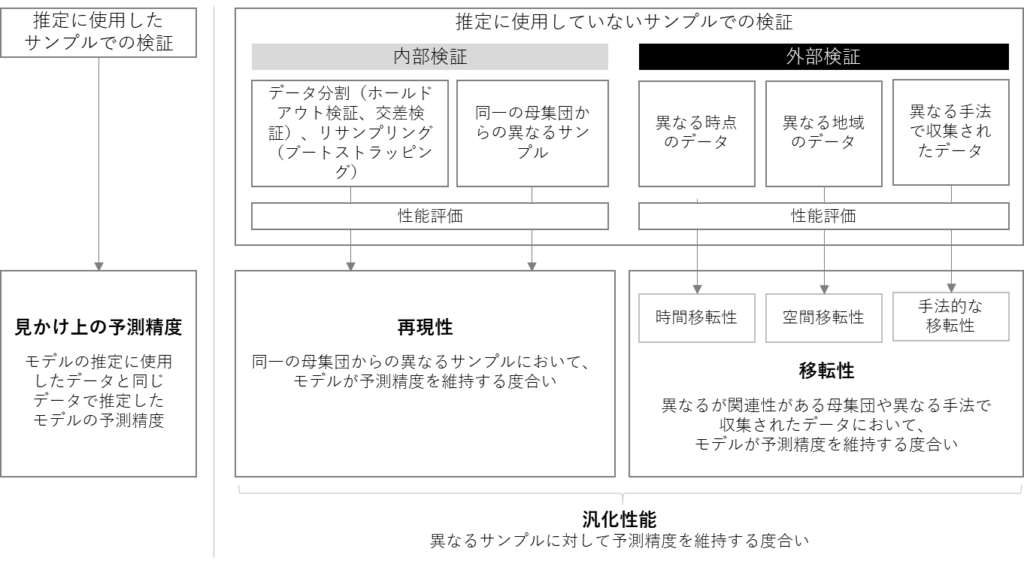
異なるデータに対しても予測精度を維持することを「汎化性能」と呼びます。この汎化性能を確保することがモデルの検証では重要となります。
汎化性能は「再現性」と「移転性」に2種類分けて考えることができます。「再現性」とは”同一の母集団からの異なるサンプルにおいて、モデルが予測精度を維持すること”であり、「移転性」とは”異なる母集団等のサンプルにおいて、モデルが予測精度を維持すること”を言います。
移転性が確保されていると、より広範囲でモデルが活用しやすいですが、移転性の検証のためには「外部検証」を行う必要があり、これには異なる時点や異なる地域のデータが必要となり、データの制約上難しい場合も多いです。
一方で、再現性を確認するための「内部検証」は1つのデータセットがあれば実施可能であることから、少なくとも内部検証による再現性の確認は実施することが必須であると、参考論文でも述べられています。
なお、推定に使用したサンプルを使って検証することは、先にも述べたように、異なるデータに対する汎化性能を検証することになっておらず、見かけ上の予測精度を見ているだけなので注意が必要です。
内部検証の方法
内部検証の方法として、データセットを推定用のデータと検証用のデータに分割して検証を行う方法と、データセットからリサンプリングをして新たにデータセットを作成する方法があります。
ここでは、前者のデータ分割の方法としてホールドアウト検証(Holdout validation)と交差検証(Cross validation)、後者のリサンプリングの方法としてブートストラッピング(Bootstrapping method)を紹介します。
ホールドアウト検証 (Holdout validation)
ホールドアウト検証では、データセットを推定用のデータと検証用のデータの2つにわけ、推定用のデータセットでモデルのパラメータを推定し、検証用のデータセットで評価指標を算出し検証をします。

ホールドアウト検証は、検証結果がデータセットの分割の仕方に依存してしまうため、次の交差検証を用いることが望ましいです。
交差検証 (Cross validation)
交差検証では、ホールドアウトを複数回繰り返すことで検証を行います。ホールドアウトを繰り返した回数分だけ評価指標が出てきますが、シンプルなケースでは、各パターンのホールドアウトの評価指標の平均を取ることで交差検証の評価指標とします。

特に、データセットをK個に分割することをK交差検証(K-fold cross-validation)と呼びます。K交差検証での評価指標は、以下のように計算できます。
$$ CV = \frac{1}{K}\sum_{k=1}^{K} \textit{HOV}_k $$
ここで、\(CV\)は交差検証の評価指標、\(HOV\)は各パターンのホールドアウトの評価指標を表します。
ブートストラッピング (Bootstrapping methods)
ブートストラッピングでは、サンプルセットからリサンプリングを行うことでサブサンプルセットを複数作成し、各サブサンプルセットに対して評価指標を算出することで検証を行います。
具体的には、サンプル数がNのデータの場合、サンプルセットからサンプル数と同じN回だけサンプリングを繰り返すことで、サブサンプルセットを作成します。(この際、同じサンプルが重複して抽出されるのを許容します)
各サブサンプルセットを用いてモデルを推定し、オリジナルのサンプルセットを検証用データとして評価指標を算出します。
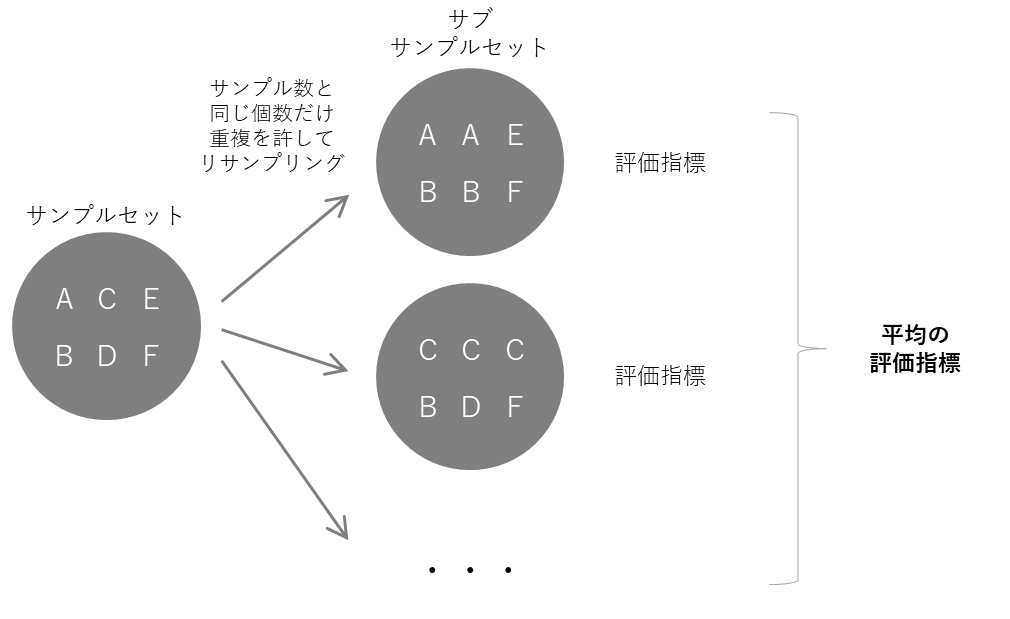
サブサンプルセットの数だけ評価指標が出てきますが、シンプルなケースでは、各サブサンプルセットの評価指標の平均を取ることで、ブートストラッピングの評価指標とします。
$$ BS = \frac{1}{B}\sum_{b=1}^{B} \textit{BS}_b $$
ここで、\(BS\)はブートストラッピングの評価指標、\(BS_b\)は各サブサンプルセットの評価指標を表します。
交差検証はサンプルサイズが小さい場合に、評価指標が大きく変動することがあるため、その際にはブートストラッピングを用いることが有効だと言われています。
検証の評価指標
モデル検証の評価指標として、よく用いられる指標を紹介します。これだけを見ておけばよいという指標はなく、複数の指標を算出し総合的に判断することが重要です。
尤度比、自由度調整済み尤度比
尤度比(別名:McFaddenの決定係数)は、モデルによってどれくらいデータを説明することができるかを表す指標であり、数値が大きいほど適切なモデルとなります。
$$ \rho^{2} = 1 \ – \ \frac{\text{ln } L(\hat{\beta})}{\text{ln } L(0)} $$
ここで、\(L(0)\)はモデルを適用しない場合の初期尤度、\(L(\hat{\beta})\)は推定したモデルパラメータ\(\hat{\beta}\)を適用した場合の尤度を示します。(尤度の説明はこちら等を参照)
尤度比は0から1の間の数値をとり、数値が大きいほどデータに対する当てはまりが良くなります。
交通手段選択モデルでは0.2~0.4程度の数値をとることが多く、0.1を切るようであるとモデルの性能が低いと判断されることが多いです。
尤度比はモデルの説明変数を増やすと必ず指標が改善するという特徴があります。説明変数の効率性を考慮するため、実際には自由度調整済み尤度比が用いられるケースが多いです。
$$ \bar{\rho}^{2} = 1 \ – \ \frac{\text{ln } L(\hat{\beta}) \ – \ k}{\text{ln } L(0)} $$
ここで、\(k\)は説明変数の数を示します。
AIC、BIC
AIC(赤池情報量基準)やBIC(ベイズ情報量基準)は、説明変数の効率性を考慮するため、説明変数の数をペナルティとして加えて尤度を評価する指標です。
$$ \text{AIC} = -2\text{ln} L + 2k $$
$$ \text{BIC} = -2\text{ln} L + k\text{ln}(n) $$
ここで、\(L\)はモデルを適用した場合の尤度、\(k\)は説明変数の数、\(n\)はサンプルの数を示します。
AICもBICも数値が小さいほど当てはまりが良いことを示しますが、数値の絶対値自体に意味はなく、この数値以下なら良いという基準があるわけではありません。
的中率
的中率は、各個人の実績の選択結果とモデルによる予測結果を比較し、予測がどれくらい当たっているかを示す指標です。
具体的には、モデルによる予測確率が最も高い選択肢と実績の選択結果が一致していれば的中、そうでなければ外れとして、全体で何パーセントが的中しているかを計算します。
$$ \frac{1}{N} \sum_{n=1}^{N} \textit{CP}$$
$$ \textit{CP} = \begin{cases} 1 \; \text{if} \; \hat{y} = y \\ 0 \; \text{if} \; \hat{y} \neq y \end{cases} $$
ここで、\(y\)は実績の選択結果、\(\hat{y}\)はモデルの予測結果を示します。
的中率は直感的にわかりやすく、交通分野でも評価指標としてよく用いられていますが、予測確率が何パーセントであったかという情報が抜け落ちてしまいます。
例えば、a, b, cと3つの選択肢があり、1つ目のモデルは34%, 33%, 33%と選択確率を予測し、2つ目のモデルは90%, 5%, 5%と予測した場合、どちらも予測結果はaとなってしまいます。本来、ほぼ等確率な予測結果である前者のモデルは性能が低く、後者のモデルの方が性能が高いのですが、的中率の指標ではそれらの違いは加味されなくなってしまいます。
そのため、前述したような尤度比等の指標に着目することが望ましいです。
予測データと実績データの比較
検証用データに対してモデルを適用して予測した選択確率と、検証用データの実績の選択確率を比較します。従来の現況再現性の検証と同じ視点での比較ではありますが、モデルの推定用データと検証用データを分けているのが重要なポイントです。
例えば交通手段の選択モデルでは、以下のグラフのように交通手段分担率の実績値と予測値を比較することを行います。
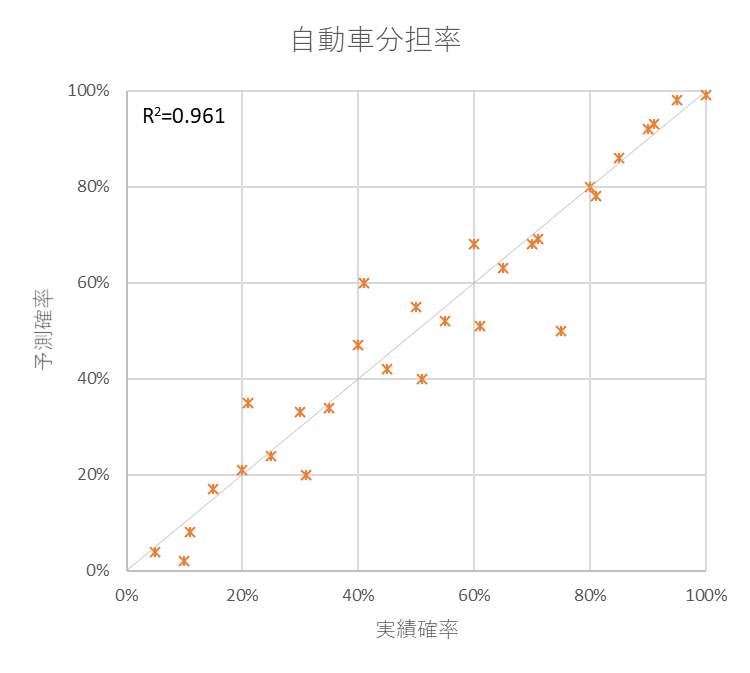
相関係数、RMSE、MAE
上記の予測データと実績データの比較を定量的に示したい場合に、相関係数やRMSE(Root Mean Square Error:二乗平均平方根誤差)、MAE(Mean Absolute Error:平均絶対誤差)などが用いられます。
相関係数は0から1の間の数値であり、数値が大きいほど、予測と実績の相関が高いことを示しています。
ただし、予測データと実績データが比例関係にある場合、相関係数では適切に評価できない場合があります。例えば、予測データが実績データに対して全て1.1倍の場合、両者に乖離はあるのですが、相関係数としては1となります。このように系統的な乖離を評価できない可能性があるので、注意が必要です。
RMSEやMAEは、予測データと実績データの乖離(予測誤差)を評価した指標です。数値が小さいほど両者の乖離が小さいことを示しています。(各指標の算出方法はこちらのサイトなどが参考になります)
誤差が正規分布に従っている場合は、RMSEによる評価が適切であると言われています。
留意点
どの評価指標を用いるか?
これだけを見ておけばよいという指標はなく、複数の指標を算出し総合的に判断することが重要です。
もちろん全ての指標で一番よいモデルが理想なのですが、実際は指標によって最適なモデルは異なるため、どの指標を重視するかを分析者側で判断し、モデルを選択する必要があります。ただし、どのような判断基準でモデルを選択したのかを明示しておくことが重要です。
データセットや検証方法の共有
第三者が検証の妥当性を判断できるように、論文やレポート内で検証方法を明示しておくことが重要です。
また、推定に用いたデータセットを明示するとともに、可能であれば公表等によりアクセスできる環境を用意することが理想です。
検証方法以外の留意点
モデルを推定し予測で用いる場合には、データ自体の持つバイアス、モデル構造の適切な選択方法、説明変数の適切な選択方法、政策効果に関する統計的検出力等にも留意する必要があります。
これらに関しては、今後別の記事で触れたいと思います。
まとめ
この記事では、モデルの未知データに対する予測精度を検証する方法を紹介しました。
モデル作成においては検証よりも推定に目を向けられがちですが、特に実務においては予測結果が都市政策や交通政策の意思決定の判断材料として用いられているため、時間をかけて適切な方法で検証することがとても重要になります。
この記事が、データに基づいたより良い意思決定につながることを願っています。



コメント