都市交通の分野でデータ活用について検討していると、重回帰分析という分析手法を提案されることや重回帰分析での分析結果を提示されることがあると思います。
重回帰分析は様々な分野で活用される手法で、都市交通の分野においてもいくつかの場面で代表的な手法として使用されています。
本記事では、重回帰分析の名前を初めて聞いた人から聞いたことがある人を対象に
- 何のために行うのか
- 何に気を付けた方がよいのか
- 都市交通では、どんな場面で使われるのか
という点について解説していきます。
重回帰分析とは
重回帰分析とは
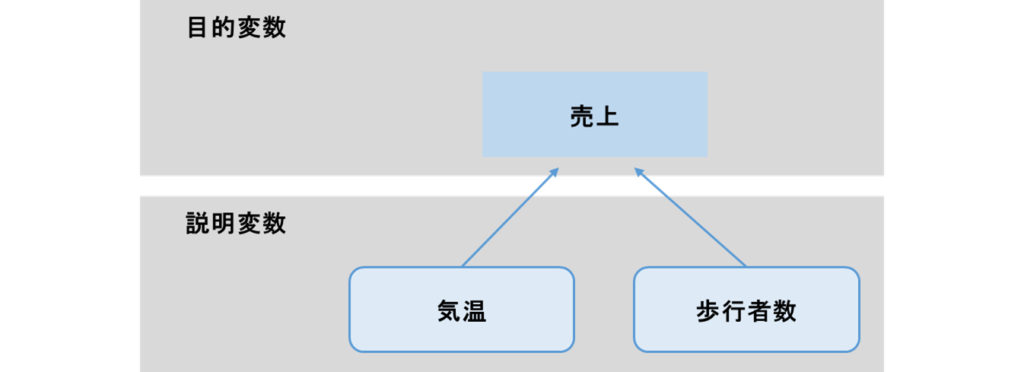
重回帰分析とは、ある結果(目的変数)について複数のデータ(説明変数)を用いて、目的変数と説明変数の関係性を分析する手法です。
例えば、あるアイスクリーム店の売上について考えるとします。このときアイスクリームの売上は、気温と店舗前の歩行者数に大きく影響されることがわかっていれば、売上と気温・歩行者数との関係性を分析することが考えられます。
重回帰分析の目的
上記で説明した重回帰分析ですが、具体的には大きく2つの目的で使用されます。
目的1:目的変数と説明変数の関係性を分析する
関係性の分析をすることで、目的変数の変化と説明変数の変化の関係性を把握します。
例えば、上記のアイスクリームの売上の例では、
- 売上と気温・歩行者数の関係性
- 気温と歩行者数の影響の大小
等について把握することを目的とします。これによって目的に対してどのような施策が有効かということについて検討を行います。
目的2:目的変数の予測をする
重回帰分析で推定した関係性をもとに、目的変数の予測を行います。
例えば、上記のアイスクリームの売上の例では、来週の天気予報の気温から来週の売上を予測する、等によって、仕入の量を考えるといった活用の方法が考えられます。
都市交通分野での利用事例
以下、具体的に交通の分野で重回帰分析が行われる代表的な事例について取り上げます。
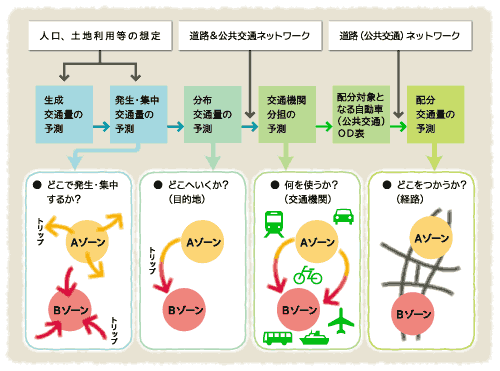
生成交通量の推定
4段階推計法において交通量予測を行う際、生成交通量を推定するのに重回帰分析を行うことがあります。この場合、地域別の生成交通量を目的変数に、各地域の特性を表現する変数を説明変数にいれて重回帰分析を実施します。
地域別の人口
地域別の人口を推計する際、重回帰分析を使用する場合があります。この場合、人口の総量を先に推計したうえで、重回帰分析にて推定された人口分布にその人口の総量を按分する形で地域別人口の推定を行います。
Excelを用いた重回帰分析の実施
本節では、実際に重回帰分析を行うことで、よりイメージを深めていきたいと思います。
データの用意
まずデータを用意します。(こちらのスプレッドシートにデータをおいてあるので、ご自由にお使いください!)
今回は、都道府県別の人口を目的変数として用意し、都道府県別の住宅数と道路延長を説明変数として用意しました。この時、目的変数として設定した変数の解像度と同様の解像度で説明変数のデータも集めることがポイントです。つまり、都道府県別の人口を目的変数として設定しているので、住宅数や道路延長も都道府県別に集める必要があるということです。
分析の実施
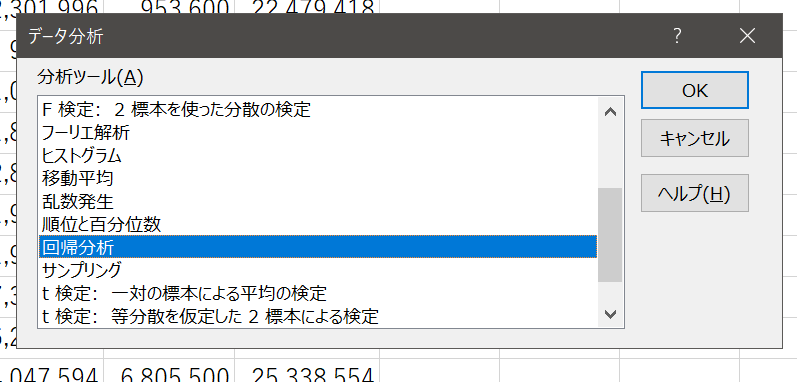
①データ分析のタブを押す
データ分析のタブを押して、分析ツールを立ち上げます

②回帰分析を選択
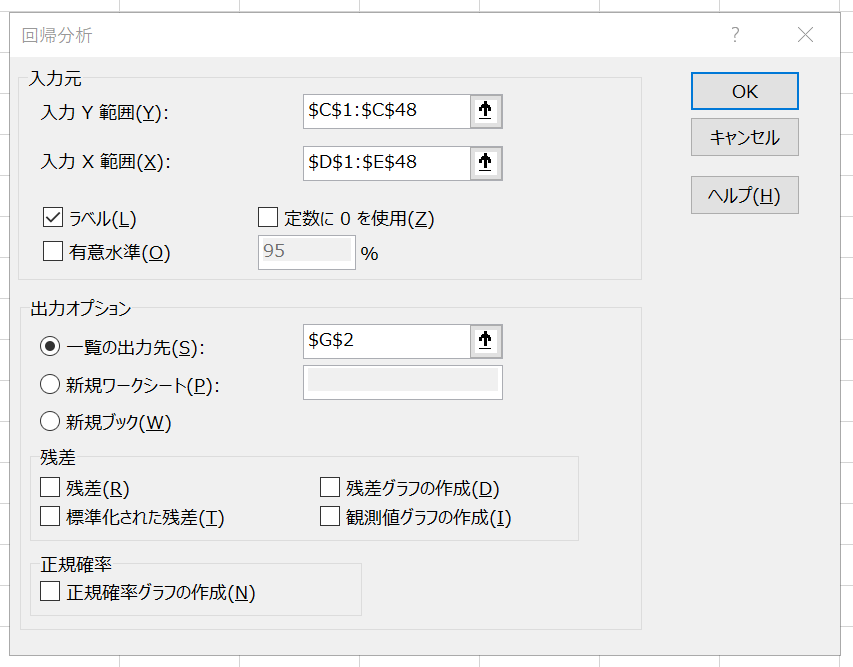
③変数の選択
目的変数を入力Y範囲に入力し、説明変数を入力X範囲に入力します。
④結果が出力される
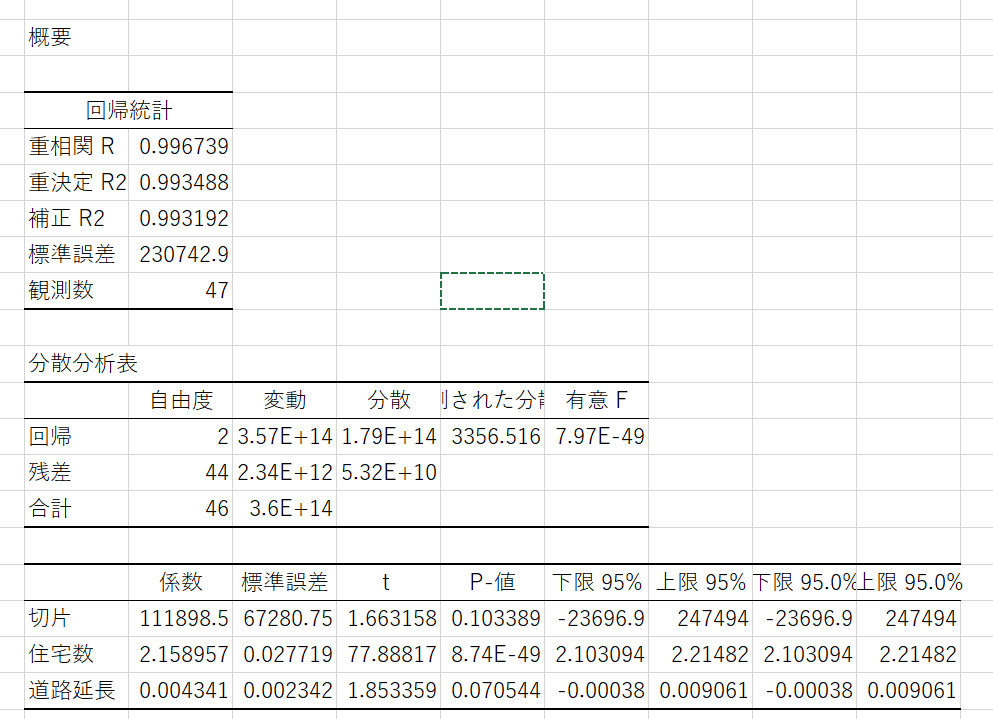
結果の解釈
解釈のポイント
重回帰分析の結果を確認する際、注意したいポイント2点のポイントを示します。
決定係数
決定係数は、重回帰分析全体の適合度を示す指標で、0~1の値をとり、高ければ高いほどモデルの適合度が高いと読み取ることができます。この値が低すぎる場合については、モデルの適合度が低く留意する必要があるという点を留意する必要があります。
P値
P値をみることで、各説明変数と目的変数の関係性が統計的に有意かどうかということがわかります。一般的に用いられる閾値は、P値の値が0.05(or 0.01)以下の場合に5%(or 1%)の確率で統計的に有意であるという見方をします。
都道府県別人口の解釈
先ほど事例に挙げた都道府県別人口の分析結果についてみると
- 決定係数は0.99と高くモデルの適合度は高いと考えられる。
- 住宅数のP値は0.01より低いので統計的に有意だと考えられる。
⇒ 係数がプラスなので、住宅数が多くなればなるほど人口も多くなる関係性にある。 - 道路延長のP値は0.05より高いので統計的に有意ではない。

重回帰分析の式
重回帰分析は、目的変数(Y)を説明変数(X)で以下のように近似できるよう、パラメータ(b)を推定します。このパラメータが、Excelの推定で出てきた係数にあたります。
$$ Y = b1×X1 + b2×X2 + ・・・ + an×Xn + b0 $$
つまり、都道府県別人口の推定式に当てはめると以下のようになり、
$$ 都道府県別人口 = b1×住宅数 + b2×道路延長 + b0 $$
推定結果を当てはめると、以下のようになります。
$$ 都道府県別人口 = 2.159×住宅数 + 0.004×道路延長 + 111898.5 $$
結果を見るときの注意点
最後に、以上でみてきた重回帰分析について、結果を確認する際の2つの注意点を整理します。
相関関係と因果関係
重回帰分析の結果をみると、いかにも目的変数と説明変数の間因果関係があるように見えてしまいますし、因果関係があるように説明してしまいがちです。しかし、厳密にこれらの間に因果関係があることは説明されていない点に注意が必要です。
多重共線性
重回帰分析を行う際には、多重共線性に気を付ける必要があります。重回帰分析において複数使用する説明変数の間に相関関係がある状況を多重共線性があるといい、この多重共線性がある場合、分析結果が適切に算出されないという問題点があるので注意が必要です。



コメント